全焊接球阀为全通径,具有较强的流通能力,阀体结构采用整体式焊接,不会出现外部泄漏等现象,球体的加工精度高,操作轻便。全焊接球阀凭借其优良的特性,广泛应用于天然气和油品长输管道。在工作过程中,球阀通过球体的转动实现启闭,阀门内部介质的流动特性影响阀门的使用寿命。流阻系数属于阀门的固有属性,只与阀门结构有关,而流量系数则比较复杂,与介质属性、介质流动状态、阀门结构等诸多因素相关。
摘 要:利用FLUENT软件对全焊接球阀(筒状)内部三维流场进行数值模拟,探究球阀从关闭到完全开启过程的流量特性。以不可压缩介质(水)为例,分析7个不同开度(10%、30%、50%、70%、80%、90%、100%)下球阀内部流场的变化情况,得到该球阀的前后压差和进出口流量,并计算得到球阀的流阻系数,然后根据相关公式求得不同开度下水的流量系数。
关键字:全焊接球阀 可压介质 流阻系数 流量系数 流量特性
全焊接球阀为全通径,具有较强的流通能力,阀体结构采用整体式焊接,不会出现外部泄漏等现象,球体的加工精度高,操作轻便。全焊接球阀凭借其优良的特性,广泛应用于天然气和油品长输管道。在工作过程中,球阀通过球体的转动实现启闭,阀门内部介质的流动特性影响阀门的使用寿命。流阻系数属于阀门的固有属性,只与阀门结构有关,而流量系数则比较复杂,与介质属性、介质流动状态、阀门结构等诸多因素相关。
随着对球阀研究的不断深入,I.Florescu等利用FLUENT对球阀不同开度下的液压能量损失进行模拟分析;ChernMing-Jyh等利用数值模拟与实验相结合的方法,得出在球阀开度为50%~100%时,加60°V型端口可以控制体积流量线性变化的结论;P.Merati等经过计算得到斯德鲁哈尔数和雷诺数之间的关系式,运用试验和CFD数值模拟验证此经验公式可用于共振的衰减;赵莹等、屈铎等利用CFD研究了球阀在不同开度下,涡流的发展变化趋势;沈新荣等利用FLUENT对球阀的流量特性进行了模拟分析;韩宁用FLUENT对特大口径环喷式流量调节阀和桁架式蝶阀进行了流场的模拟,并深入研究了阀门结构和流阻特性。上述研究均是针对不可压介质展开的,目前对可压介质的研究分析相对较少。本文利用流体动力学和FLUENT,模拟研究球阀在不同开度、不同介质下的流动特性,并根据相关公式拟合转化得到可压介质流量系数和流阻系数与开度之间的关系曲线。
1 数值模型的建立
1.1 几何模型
全焊接球阀装配体模型如图1所示,阀体进出口直径及球体直径均为1.166m,阀门腔体总长度为3.098m,阀座前后腔体长度均为801mm,介质为水和天然气,高压介质从左侧流入,右侧流出。

图1 全焊接球阀三维装配体结构图
运用SolidWorks软件分别建立开度为10%、30%、50%、70%、80%、90%和100%的流道模型。由于阀门结构对称,故模型只取一半进行计算,以有效提高计算效率,之后运用前处理软件Gambit,采用结构网格和非结构网格的混合网格画法,对全焊接球阀流道模型进行网格划分,50%开度的流道模型及网格图如图2所示。
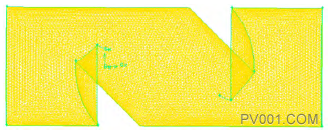
图2 50%开度的流道模型及网格图
1.2 数学模型
1.2.1 质量守恒方程(连续性方程)
质量守恒方程可以描述为单位时间内流入控制体的质量等于控制体内质量随时间的变化量,由此得出质量守恒方程的积分式为
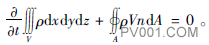 (1)
(1)
式中:V为控制体;A为控制面。
根据奥高公式,连续性方程在直角坐标系下的微分形式为
 (2)
(2)
式中:ux、uy、uz分别为x、y、z方向的速度分量,单位为m/s。
1.2.2 动量方程
动量方程本质上遵循牛顿第二定律,可以概括为:对于给定的流体惯性系统,在单位时间内系统的动量变化量等于该系统所受各作用力之和。动量方程可表示为:
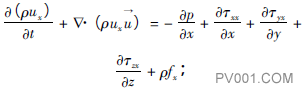 (3)
(3)
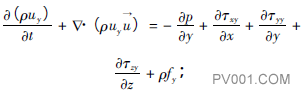 (4)
(4)
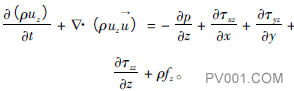 (5)
(5)
式中:fx、fy、fz分别为x、y、z方向上的单位质量力,m/s2。
1.2.3 湍流模型
在标准k-ε双方程模型中:计算压力与速度耦合项时采用SIMPLE算法;在初次计算时,k方程、ε方程及动量方程采用一阶迎风格式;二次精确计算时,采用二阶迎风格式。
2 FLUENT仿真模拟及结果分析
2.1 设置边界条件
进行流体计算时,进口为压力进口,数值为10.2MPa,出口为压力出口,数值为10.1MPa,设置对称面为symmetry,其余面设置为壁面(wall)。
2.2 FLUENT仿真模拟结果分析
由于阀门在各个开度下的流动状态比较相似,所以仅取几个有代表性的开度显示阀内的流场分布。
1)当阀芯开度为10%时,阀门开度很小,阀门进出口压差很大。阀门开度为10%的压力分布图如图3所示。可以看出,从阀门入口到阀芯再到阀门出口,其压力呈三阶式分布,入口大,中间次之,出口最小。阀门开度为10%的速度矢量图如图4所示,当阀门开度较小时阀体内流体有一定的回旋搅动,但无明显的大涡出现。

图3 10%开度的压力分布图

图4 开度为10%的速度矢量图
2)当阀芯开度为30%时,阀门开度有所增大,阀芯内压力出现变化。值得引起注意的是,由于受到入口流体的冲击,阀芯部分出现了局部的高压区域。阀门开度为30%的压力分布图如图5所示。阀门开度为30%时流体速度矢量图如图6所示,流体在阀芯中以较大涡的形式在流动。这是由于阀芯内部空间较大,流体沿着一侧流动,形成稳定的涡旋状流场。
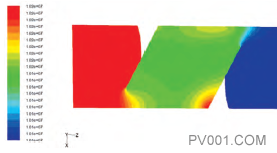
图5 开度为30%的压力分布图

图6 开度为30%的速度矢量图
3)当阀芯开度为100%时的压力云图如图7所示,速度矢量图如图8所示。阀门全开时流道为一直管,所以流速比较均匀。在靠近壁面区域速度有较大梯度,这是边界层所形成的速度衰减;流体速度方向完全一致,这也是球阀所特有的小阻力特性的表现。
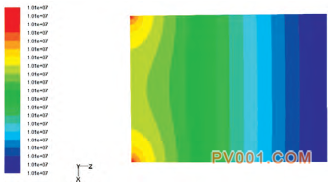
图7 开度为100%的压力分布图

图8 开度为100%的速度矢量图 ♂
3 计算流阻系数及流量系数
3.1 流阻系数
阀门在一定开度下的流阻系数是一个定值,只与阀门的结构有关,与介质类型没有关系,所以以水为介质求解流阻系数,流阻系数公式为
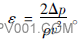 (6)
(6)
式中:Δp为阀前后压差,Pa;ρ为水的密度,kg/m3;υ为阀的出口速度,m/s。
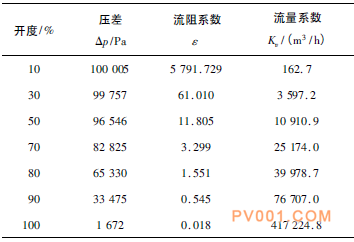
根据FLUENT运算结果,可知阀门前后压差、阀门出口速度,将其代入式(6)解得到各个开度下的流阻系数,如表1所示。
表1 介质为水时不同开度下FLUENT运算数值结果
3.2 流量系数
当阀门前后压差为100kPa时,流量系数Kv就等于体积流量Qv。体积流量Qv的计算公式为
 (7)
(7)
式中ε为阀门的流阻系数。
不可压流体流量系数计算公式为
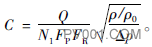 (8)
(8)
式中:FP为管道几何形状系数,无附接管件时,FP=1,量纲一;FR为雷诺数系数,在紊流状态时,FR=1,量纲一;ρ/ρ0为相对密度,在15.5℃时,ρ/ρ0=1;当长度单位为mm,压力单位为kPa,密度单位为kg/m3,流量系数用K表示时,N1=0.1。
当介质为水(不可压)时,将FLUENT后处理结果代入式(8)得到此球阀在各个开度下的流量系数,并且在10%开度时验证了当阀门前后压差为100kPa时,流量系数Kv就等于体积流量Qv,数值为162.7m3/h,如表1所示。
当介质为天然气(可压)时,流量系数的计算是在不可压介质运算结果的基础之上,经过密度比转换而得到,计算结果如表2所示,转换公式为
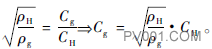 (9)
(9)
式中:Cg、CH为天然气、水的流量系数;ρg、ρH为天然气、水的密度。
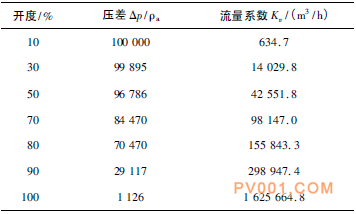
表2 介质为天然气时不同开度下的FLUENT运算数值结果
3.3 流量系数与开度的关系曲线
根据表1、表2的计算结果,可以得到开度与流阻系数的关系曲线,如图9所示,开度与流量系数的关系曲线,如图10所示。
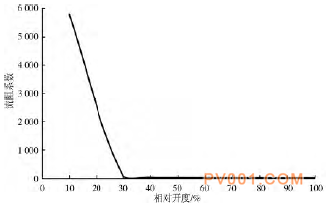
图9 开度与流阻系数的关系曲线
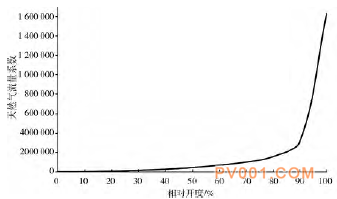
图10 开度与流量系数的关系曲线
可以看出,随着球阀开度的增大,流阻系数和流量系数均随之改变。其中:在开度10%到30%之间,流阻系数快速下降,在30%至全开,流阻系数变化速率趋于平缓,全开时球阀流阻系数为0.018,这表明阀门能量损失小,体现了球阀小阻力的特性;流量系数在开度10%到60%之间增加平缓,在80%时流量系数发生突增,全开时达到最大,此变化趋势符合球阀的工作流量特性。
4 结论
1)在阀门开度为10%时计算得到体积流量与流量系数相等,满足流量系数的定义,说明FLUENT的分析结果能与现实很好的吻合,可以用在阀门内部流场和相关参数的分析中,为理论设计和优化提供可靠数据。
2)在阀门的开启过程中,球体后会有涡流产生,开度增大时涡流逐渐变大,强度减弱,能量耗散减小。小开度时在球体和阀座之间流速较大,压力较小,若压力低于水的饱和蒸气压时,会出现空化现象,影响阀门的使用寿命。
3)可压缩介质流量系数,是在分析计算不可压缩介质流量系数的基础之上,通过密度比转换而得到,计算结果符合实际应用。

会员咨询:
客户服务:
友情链接:


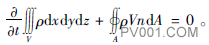 (1)
(1)  (2)
(2) 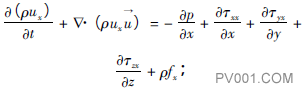 (3)
(3) 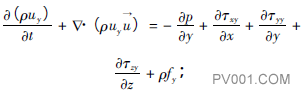 (4)
(4) 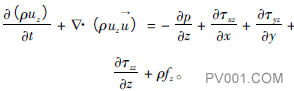 (5)
(5) 





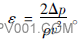 (6)
(6) 
 (7)
(7) 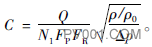 (8)
(8) 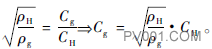 (9)
(9) 

