阀门作为流体的限制开关设备产生的最明显的一个问题是噪声,阀门噪声和伴生的振动会影响阀门性能并且会造成阀门及邻近管路及设备的疲劳,降低其使用寿命。因此,阀门噪声必须重视。
根据产生机理阀门产生的噪声分为机械振动噪声,气蚀噪声和流体噪声。
机械振动噪声是由湍流、压力振荡或由于速度和(或)大的流量所产生的不稳定的流动力量所引起的。其噪声级比较低,很少超过90dB(A),频率在50Hz~1500Hz范围之内。通过改变阀芯形状的办法,机械振动噪声往往是可以降低的。
气蚀噪声是气蚀严重程度的函数,所产生的噪声类似于纯闪蒸液体的噪声。气蚀噪声的形成机理比较复杂,目前还不能较好的预测。气蚀噪声一般不会超过100dB(A)。通过适当选择隔声材料可以处理这种噪声。
流体噪声是管路最常见的噪声源。这种噪声基本上是由于湍流流体和在混合区域内的层流流体的相互作用或者由于高速和(或)气体质量流率的冲击波所引起的。当管路流速超过声速(340m/s)时,会有较大的流体噪声,而当质量流量较大时,在较低的压降和流速下也可能产生高的噪声级。
1 阀门管路流动噪声研究方法
对于阀门管路的流动噪声,一般有两类预测方法。一类方法是经验方法,只要知道管路的几何尺寸和流动状态,就可以基于半经验公司对阀门和管路的流动噪声进行预测。目前每个大的阀门生产商基本都有自己的流动噪声预测程序。一些国际和行标也定义了流动噪声的预测方法,如IEC和ISA,其中IEC534-8-3空气动力学噪声标准是控制阀领域使用的最广的工业阀门噪声预测标准。这一标准计算流体在各个方向的声响效率因素,并可计算阀门内部的声源强度,管路的传递损失,峰值频率以及管路辐射。
此类半经验方法的优点在于计算迅速,也有一定的准确性,可作为设计的参考。其缺点在于无法详细考虑流动和管路结构对最终噪声辐射的声响,也无法处理非标准的阀门。
另一类的计算方法是使用瞬态计算流体力学(CFD)方法和声学软件结合的预测方法。通过使用CFD瞬态计算提取的信号,转换得到的等效流体声源,并加载到声学和结构模型中,计算传递损失和外场的声辐射。此类计算方法的计算量非常大,对计算资源和工程师的技术要求相对较高。其优点是可以考虑较多的细节,如流态、几何尺寸。同时计算的结果输出丰富,可以帮助工程师更好的理解流动噪声问题。
2 采用的计算方法介绍
本文使用了两种计算方法对控制阀门的流动噪声进行了预测。一种是前面介绍的基于瞬态CFD和声学软件的方法。另外一种则是将稳态CFD计算与IEC534-8-3的规范相结合,进行阀门管路噪声的预测
2.1 几何模型与求解器选择
在CFD计算中,边界位置的设置和边界条件的设置往往对计算的结果产生较大的影响。入口的位置和边界条件影响更大。入口的的速度分布和湍流度会直接影响到下游的流场。本文的模型边界为从阀门管路上游300mm到阀门管路下游900mm的部分。
对于阀门内流问题,由于管内最高速度可以超过音速,因此选择耦合式求解器进行稳态和瞬态的计算。耦合式求解器的一个好处是:其收敛速度不会随着网格的增加而变差,也就是说其计算时间基本上跟网格的数量成正比。
2.2 瞬态计算方法介绍
通过耦合CFD软件STARCCM+与专业声学软件LMSVirtual.LabAcoustic来求解阀门内部流场以及引起的外部辐射噪声。在CFD计算中,对阀门内部的瞬态流场进行求解并输出流场特征,然后将噪声的源项导入到LMSVirtual.LabAcoustic来计算噪声的传播;
计算采用三维、瞬态的耦合求解器,使用空间和时间2阶离散格式,湍流模型采用基于SSTk-w的DES模型。DES/LES是一种空间滤波的处理方法,对于大于某尺度的涡,使用DNS方法模拟其输运;对于小于该尺度的涡,则使用湍流模型来模拟其耗散。采用DES的目的是为了捕捉中高频的阀门流体噪声。
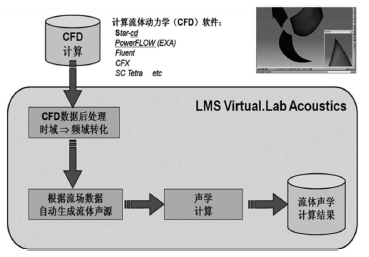
图1 瞬态CFD计算阀门噪声仿真流程
计算模型中网格的尺度往往最终受限于计算资源。采用的CFD模型网格数目为1200万左右,主要集中在阀门后部及其下游的关键区域。
基于流场计算得到的速度和压力脉动,应用经典的的Lighthill公式计算四极子声源的强度如下
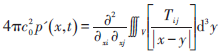 (1)
(1)
上式中Tij为Lighthill张量
在所使用的声学软件LMSVirtual.Lab中,可以自动实现基于流场数据(cgns格式)转化等效声源,并进行后续的声场计算。
2.3 稳态计算方法介绍
传统的基于稳态的阀门流体噪声计算程序,如IEC,ISA等,可以方便的基于阀门的几何尺寸和流动参数来预测阀门的辐射噪声,其一般流程如下:
1)根据几何尺寸和流态来确定阀门管道系统内流体的机械能;
2)基于经验公式确定转换系数,由流体的机械能得到流体的声能;
3)根据流体的声能,确定管路内部流体的等效总声压;
4)根据管路的材料和尺寸,计算出管路的声传递损失和管路外壁面声压;
5)计算距离管壁1m处的声压,并进行记权处理。
本文采用的稳态计算方法在确定声源强度时采用了稳态CFD预估的方法。而对声场向下游的传播,管路的隔声以及管路的声辐射,采用了与IEC类似的经验公式进行计算。这是因为使用CFD工具,基于流场的湍动能参数,可以较好的预测局部的声能量密度。但是对于目前的CFD计算格式,预测微小信号(声信号)在流场中的传播,乃至预测声场与管路结构的耦合仍然是极为困难的。
稳态计算的另一个好处是不需要提取流场的瞬态信号,可以直接使用时间平均的稳态结果,这大大降低了对计算资源的要求,提高在工程应用上的可用性。
流场计算完毕后,预估声源强度的公式如下
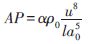 (2)
(2)
上式中AP为声功率密度,α为常数,u为速度矢量分量的均方根值,l是局部流场特征尺度,po和a0分别为远场的介质密度和声速。
流道中的总声功率计算完毕后,可带入到计算程序中,计算距离管壁1m处的记权声压级。
3 计算结果与分析
3.1 瞬态计算结果
计算得到的瞬态流场计算结果如式(2)所示
由图2可见,对于计算工况,流路内部局部最高速度达到了500m/s,超过了音速,这是由于阀门泄露处的截面类似于一个C—D喷口。经过阀门加速后的气体在扩张段中心形成了对冲,往下游逐步发展为平均流动。

图2 阀门后部下游的瞬态速度和压力分布
工质经过阀门加速后产生了过膨胀。在阀门下游处形成了激波网格结构(shock-cell)。阀门下流场的剧烈变化会对阀门结构产生强烈的冲击,导致阀门管壁振动并向外辐射噪声。
将流场信号转化为等效声源后,输入到声学软件中进行声振耦合计算,以得到阀门下游管路1m处的声场。典型的声场分布如图3所示。

图3 4000Hz管道外部声压分布
将计算的结果与测试结果相比较,见图4和图5。可见在能量最集中的频段(1000Hz~4000Hz),仿真与试验结果吻合的较好。在低频段和高频段,仿真结果比实验结果较小,这是因为对于管路传递损失,低频主要是强度控制区,建模的细节和边界条件影响很大;而对于高频,想得到准确的声源特性对CFD的要求极高,由于计算资源和计算时间的限制,导致声源的高频特性与真实情况差别较大。
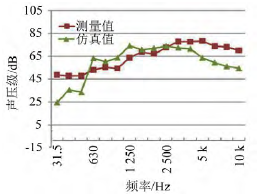
图4 1/3倍频程声压测结果比较(测点1)
计算得到三个测点的总声压级接近,测点1、测点2、测点3(测点1、2、3的位置均位于阀门下游1m处的横截平面上,距离管壁的距离均为1m)的总声压级分别为80.6dB(A),80.4dB(A),80.6dB(A)。试验得到的测点1和测点2的总声压级分别为84.6dB(A)和80.8dB(A)。对测点1和测点2,计算与仿真的误差分别为4dB(A)和0.4dB(A)。
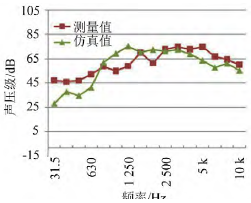
图5 1/3倍频程声压测量结果比较(测点2)
3.2 稳态计算结果
使用稳态方法进行计算,首先使用稳态CFD计算,得到阀门管道流场中的声功率密度如下图6所示。

图6 流道内声功率密度分布
由图可见,局部声功率最大的地方存在与阀门后部下游的激波区和混合区。
将计算得到的流场的总声功率值代入计算程序(实现IEC-534-8-3和ISA规范),得到的计算工况试验与仿真结果的对比如图7。
由图7可见,对于计算工况,在300Hz到10000Hz的范围内,稳态CFD方法的预测曲线与测量曲线的趋势基本一致,幅值差距也较小。

图7 1/3倍频程声压测量结果比较
4 结语
通过两种方法的计算,可以得到的结论如下:
(1)两种方法均可以较好的预测调节阀门的噪声。通过与测量结果的比较,稳态方法预测结果和瞬态方法预测结果的趋势均与测量结果曲线基本一致,验证了两种预测方法的可靠性;
(2)瞬态计算方法的计算流程比较简单,但是计算量相较稳态计算要大两个数量级以上;
(3)稳态计算方法计算量小,预报精度与瞬态方法相当,具有很大的工程价值。

会员咨询:
客户服务:
友情链接:

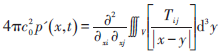 (1)
(1)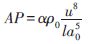 (2)
(2)




