流固耦合技术在水轮机蝶阀活门动态特性分析中的应用

        1 概述
        水轮机蝶阀的活门是水轮机的重要部件。活门在关闭位置时，承受全部水压力；在全开位置时，处在水流中心，因此，活门需要足够的强度和刚度。同时，活门处于开启位置时，来水要经过活门，产生的流体紊乱会导致活门的振动，因此要求活门具有良好的水力性能。
        本文利用有限元分析软件ADINA，采用直接耦合的方法，对某型号活门进行动态特性分析，求解活门在流体中的固有频率；根据计算结果，进行结构上的优化，从而确保流体的激振频率远离活门的固有频率，可以保证活门在开启状态下，不会因为卡门涡，造成活门振动加重，甚至出现裂纹破坏。
        2 数学模型
        流固耦合的主要表现为：流体的流动作用在结构表面，构成结构流体边界，引起结构的变形振动；同时结构变形改变流体的流动空间，构成新的流体的运动边界，导致流场变化。这两种介质的相互作用耦合在一起，构成一个整体。
        2.1 不可压缩黏性流体流动的有限元方程
        不可压缩黏性流体流动的连续方程和Navieostokes方程

        
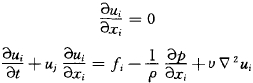
        将计算区域分为有限多个单元，可以得到相应的有限元方程

        
        式中：各个下标α、β、γ=1、2、⋯、r（r为单元的节点总数），各系数阵的上标和变量的下标i、j、k=1、2、3，分别代表空间坐标x、y、zo
        应用相同的方法可以导出关于连续方程的单元，有限元方程

        
        将有限元方程按计算区域根据一定的方式迭加起来，便得到了关于求解不可压缩薪性流体流动的总体矩阵方程如下

        
        2.2 弹性结构体的有限元方程
        动态中单元的运动方程为

        
        结构整体的运动方程式可以用单元的运动方程作为基础，按一定的方式叠加而得到

        
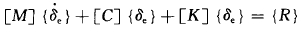
        结构整体的有限元方程为

        
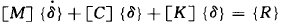
        2.3 流固藕合的有限元方程
        考虑流体的作用，弹性体在流体中离散后的结构动力学方程应该写成

        
        其中，F（t）为节点外加载荷向量，Rt（t）为流体与结构相互作用而产生的附加节点向量，它们都是压力P的函数。
        所以可以写成

        
        在流动水场中，求解流体弹性问题的扰动流程不仅与弹性体的变形有关，还与初始流动水场的速度有关。这时水压力不仅产生了附加质量，还产生了附加阻尼项和附加刚度项，流固耦合问题的物理实质是联合求解方程组

        
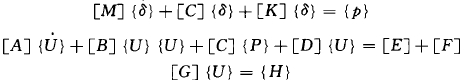
        3 计算结果
        利用有限元分析软件ADINA，进行水轮机蝶阀活门的动态特性分析，首先计算活门在空气中的固有频率，同时计算活门在流体中的固有频率，比较活门在两种介质中的动态特性的差异。活门计算有限元模型见图1。

图1 活门计算有限元模型

        3.1 活门在空气中的动态特性
        首先计算活门在空气中的固有频率，如图1-图6所示。

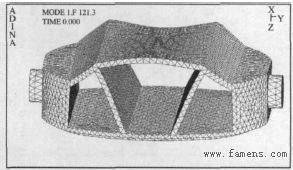
图2 活门第一阶固有频率（空气中）

图3 活门第二阶固有频率（空气中）

图4 活门第三阶固有频率（空气中）

图5 活门第四阶固有频率（空气中）

图6 活门第五阶固有频率（空气中）

        3.2 活门在水中的动态特性
        采用ADINA的流固耦合技术，计算活门在水中的固有频率。计算模型的网格与计算空气中活门固有频率一致，考虑流体的附加质量和附加刚度，水中结构件的固有频率会有改变，改变的幅度，也在计算中得到体现。如图7-图11所示。

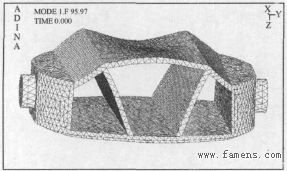
图7 活门第一阶固有频率（水中）

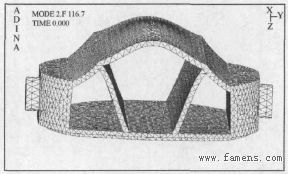
图8 活门第二阶固有频率（水中）

图9 活门第三阶固有频率（水中）

图10 活门第四阶固有频率（水中）

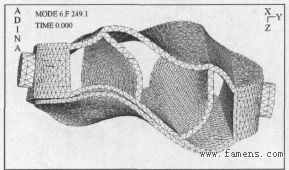
图11 活门第五阶固有频率（水中）

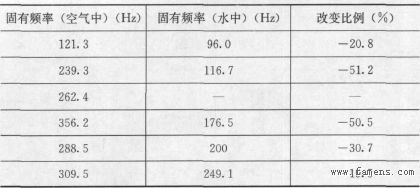
        针对同一振型的固有频率，得到表1所列结果。

表1 固有频率结果

        3.3 计算结果
        经过计算，活门在流场中的固有频率比空气中的固有频率有所下降，而且，对于不同的振型，固有频率下降幅度不同；模型振型阶数发生变化。
        4 结论
        利用有限元分析软件ADINA，对某型号的水轮机活门进行了动态特性分析。采用流固耦合方法，求解了活门在空气中和流体中的固有频率，改进了已有的求解方法，从而，能够更好地避免活门出现涡流振动的情况。
        计算说明，采用流固藕合技术才能准确的计算活门的固有频率，从而为活门结构的设计、优化及水轮机振动故障的诊断，提供了理论指导。
        参考文献
        [1]巴斯.ADINA使用手册——自动动态增量非线性分析有限元程序.北京：机械工业出版社，1986.
        [2]刘延柱.振动力学.北京：高等教育出版社，1998
        [3]白莱文斯.流体诱发振动.北京：机械工业出版社，1983.
        [4]屠大燕.流体力学与流体机械.北京：中国建筑工业出版社，1994