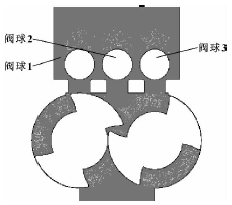
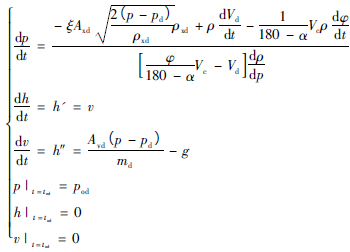转子泵出口球阀动态特性计算与分析
作者:张生昌 杨琳 邓鸿英 马艺 王炤东
2015年01月14日 来源: 浏览量:
字号:T
|
T
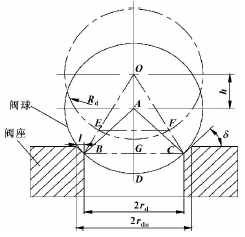
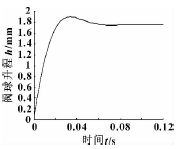
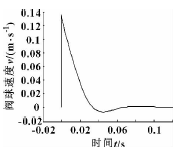
长期以来,国内外出现了很多种油气混输泵,有螺杆泵、轴流泵、液环泵、叶片泵、转子泵等。但在含气量较大工况时,上述油气混输泵极易产生气阻失效。针对传统混输泵产品存在的缺陷,提出了一种新型内压缩转子式油气混
全球阀门网(www.famens.com )友情提醒,转载请务必注明来源:全球阀门网!违者必究.
相关新闻
免责声明:1、本文系本网编辑转载或者作者自行发布,本网发布文章的目的在于传递更多信息给访问者,并不代表本网赞同其观点,同时本网亦不对文章内容的真实性负责。
2、如涉及作品内容、版权和其它问题,请在30日内与本网联系,我们将在第一时间作出适当处理!有关作品版权事宜请联系:+86-571-88970062
2、如涉及作品内容、版权和其它问题,请在30日内与本网联系,我们将在第一时间作出适当处理!有关作品版权事宜请联系:+86-571-88970062
推荐新闻

用户找,扫一扫!
关于我们 - 刊登广告 - 会员服务 - 企业建站 - 积分服务 - 企业名录 - 法律声明 - 本网动态 - 阀门地图sitemap
广告热线:0571-88970062 服务热线:0571-56077860 传真:0571-88971936 邮箱:sales#famens.com
广告咨询
会员咨询:
客户服务:
友情链接: