采用计算流体力学软件对蝶阀阀体后双弯管道模型中的复杂流动现象进行了数值模拟,对比分析了进口雷诺数和阀门角度变化对流场的影响。通过与扭矩实验测量结果比较优选出SST湍流模型,并进一步模拟各种工况下管道内部的流场。结果表明:进口雷诺数对流场的影响是定量的,随着进口雷诺数的增大,扭矩值增大,阀板迎流面前驻点保持不变,背流面一、二次流动分离区不断减小;阀门角度对流场的影响是定性的,这种影响可通过流动分离、弯管二次流以及流动剪切碰撞等理论来解释;在所选4种阀门角度中,角度越大,阀门对流动阻挡作用越大,阀板前驻点逐渐向阀板中心移动,背流面更易产生一、二次分离区;阀门角度从30°变为45°时,相关参数急剧变化,同时发生较显著的一、二次流动分离现象。
由于结构简单、操作方便,蝶阀作为流动控制与调节的设备在动力工程、城市供水、化工和船舶等工业场合应用广泛。然而,在调节蝶阀阀门角度以实施流动控制时,蝶阀阀板下游常常出现较大流动分离,容易诱发噪声辐射和结构振动等不利现象。布置在长直管内部的蝶阀流动分离现象已经得到了非常广泛的重视和研究。然而,在某些特殊场合,由于空间布置限制等原因,蝶阀常常需要和弯管就近配合使用,这使得蝶阀和弯管复合系统内部的流动现象更加复杂。因此,对蝶阀弯管系统内部的复杂流动现象进行系统研究是很有必要的。
笔者采用计算流体力学CFD手段对某蝶阀阀体后双弯管道系统中所存在的复杂流动现象进行了系统的数值模拟和分析,重点对比分析了进口雷诺数和阀门角度对阀门下游流场的影响。
1 扭矩测量实验
笔者所选的蝶阀阀体后双弯管道模型是对某电厂汽轮机系统中低压缸间抽汽管道进行的一定几何相似缩比模型,如图1所示。图1中管道横截面直径d=100mm,阀门角度定义为来流与阀板迎流面夹角(锐角)θ,其范围为0°~75°。
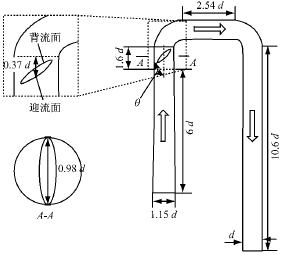
图1 数值计算模型示意图
为优选合理的湍流模型并验证数值模拟扭矩计算结果,笔者建立了阀板扭矩测量实验系统,如图2所示。测量时,通过变频仪调节电机转速以改变高压风机的吸气压力,达到调节系统进口空气质量流量的目的,同时通过静态扭矩传感器测量不同工况的阀板扭矩值。进口空气质量流量的具体获得方法如下:通过喷嘴流量计和微测压计测得进口处与当地大气压压差,并通过温湿度计测量实验当地当时的室温和湿度,气压计读出当地大气压,在此基础上,计算得出模型进口空气质量流量。实验时阀门角度范围为-75°~75°,扭矩测量范围为-0.52~0.47N•m,进口空气质量流量范围为0.02~0.472kg/s。

图2 实验测量系统示意图
2 湍流模型选择
选择阀门角度为45°时的最大进口雷诺数工况进行湍流模型的比较和选择,此时进口空气质量流量为0.381kg/s,相应Re为2.39×105。
采用商用计算流体力学软件Ansys CFX14.0实现流场稳态计算。基于几何模型结构的对称性,并结合相关比较分析,实际计算区域仅取原始模型的一半,以避免计算网格数量过多带来的诸多不利。采用稳态时均和对称算法可解决具有一定非稳态效应的流动问题,同时满足实际工程应用中对时均量的要求。采用ICEM CFD 14.0实施混合网格划分,其划分策略见图3,并使近壁面网格满足y+<2。选取RNG k-ε(scalable wall function壁面函数)、standard k-ε(automatic near-wall treat-ment壁面函数)及SST(automatic near-wall treat-ment壁面函数)3种湍流模型进行比较选优。
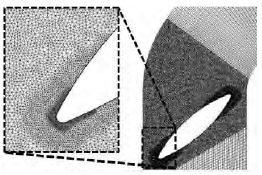
图3 网格划分
流动控制方程组由可压缩流动雷诺方程、理想气体状态方程和各湍流模型方程组成。空气介质按理想气体处理,参考压力为97 856Pa,并考虑黏性耗散效应。离散方程采用有界高精度对流格式求解,并通过Rhie和Chow算法计算空气质量流量,以保证压力和速度耦合.在299K和5%湍流度下,给定进口总压为590.01Pa,给定出口空气质量流量为qm=0.190kg/s,且速度和温度分布满足局部单向化假设;阀板面用丙烯黑色颜料作涂黑处理,故设置为无滑移绝热边界条件;因实验管道材料(即有机玻璃)导热系数较小,故管道壁面设置为无滑移绝热边界条件;对称面(图1中平行纸面方向所取的中截面)设置为对称边界条件。分别在阀板迎、背流面及两弯管内侧附近各选定一个速度监控点,残差标准设为10-5,且网格无关性验证指标选择为阀板扭矩值是否随网格数增加而变化。此处扭矩表示流体对指定二维区域(这里指阀板面)作用力相对特定轴(这里指穿过阀板中心且垂直纸面的轴线)产生的力矩;对壁面边界条件而言,作用力为气体压力和黏性切应力之和在所选面上的积分;具体计算过程通过软件中相关函数实现。
通过比较各湍流模型的扭矩计算结果,在同等数量的网格下,SST湍流模型更能获得与实验测量结果相符的扭矩值,此时网格总数量为809万。出于篇幅考虑,具体比较过程省略。
3 结果与分析
3.1 进口雷诺数的影响
基于实验测量获得的阀门角度为45°下不同进口空气质量流量及其扭矩值,本节通过数值模拟的方法研究进口雷诺数变化对流场的影响,并将计算所得扭矩值与实验测量扭矩值进行对比验证。网格划分、边界条件等与第2节类似,结果见表1。
表1 阀门角度为45°时不同进口雷诺数下扭矩计算值与实验值的对比

由表1可知,数值计算获得的扭矩值与实验测量值基本相符,从而在一定程度上验证了本文计算的准确性,且扭矩值随进口雷诺数增大而增大。
图4给出了阀门角度为45°时不同进口雷诺数下中截面阀板周围速度矢量图。由图4可知,随进口雷诺数的增大,中截面阀板周围速度矢量图基本一致,阀门角度对流场的影响是定量而非定性的;通过其他参数分析也可得到相同结论,限于篇幅不再阐述。经实际测量可得,随着进口雷诺数的增大,迎流面前驻点p位置几乎不变,但背流面一、二次分离区(L1和L2)不断减小。前驻点x轴的坐标为-0.21d(以垂直来流方向为x轴,规定x轴与阀板和管道中心线交点为坐标原点,图4中向右为正、向左为负),且一次分离区再附点坐标从-0.11d变为-0.16d。定义阀板背流面因来流攻角造成的前端分离现象为一次分离区(L1),而阀板背流面与管道间通流截面扩张引起逆压梯度而造成的流动分离为二次分离区(L2)。

图4 阀门角度为45°时不同进口雷诺数下中截面阀板周围速度矢量图
3.2 阀门角度的影响
基于阀门角度为45°时的最大进口雷诺数,将其应用于其他阀门角度(0°、15°和30°)工况,并通过数值模拟方法研究阀门角度变化对流场的影响。网格划分等与第2节相似。
3.2.1 中截面及各剖面速度矢量图
为研究阀板周围复杂的三维流动,首先研究中截面及相关剖面的速度矢量图.所选4个剖面(沿来流方向依次命名为Slice-1到Slice-4)位置如图5所示,对应图5中A-A、B-B、C-C和D-D视图。不同阀门角度下各剖面的速度矢量图见图6。
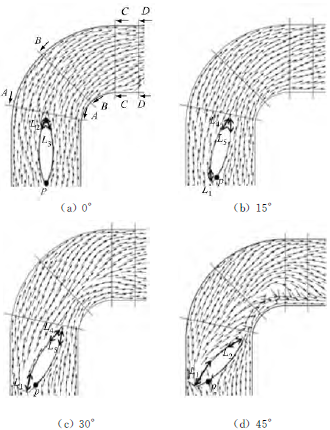
图5 不同阀门角度下中截面速度矢量图及流动分离分析
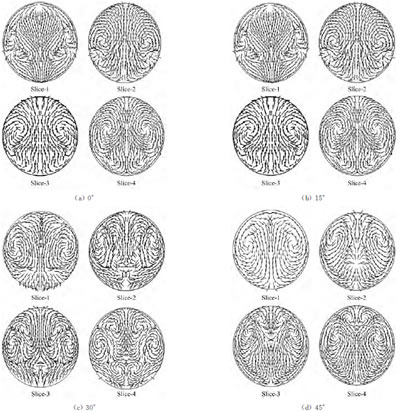
图6 不同阀门角度下各剖面的速度矢量图
当阀门角度为0°时,均匀来流经过阀板与管道间时,由于通流截面扩张缓慢,逆压梯度较小,因而没有发生明显的流动分离。从Slice-1可知,该剖面中心线上速度矢量呈现“上部向下,中部向上和下部向下”的趋势;其上、下部均向下是管道内外侧压力作用下流体质点向心运动的表现,而中部向上则是阀板右侧通流截面扩张段对流动向管道外侧引导的表现;中心线向上运动的流体质点两旁是流团向中心的运动,这是阀板与管道间通流截面扩张段对流体质点向中央的引导和通过阀板后通流截面增加引起流体质点横向流动的表现,亦是阀板对流动阻挡作用的必然结果。随着流体质点继续向后流动,Slice-2和Slice-3上中心线速度矢量均向上,这是流体质点离心运动的结果,因为此处径向压力梯度不足以提供流体质点向心运动所需的向心力,而Slice-4中流动则包含了弯管内侧流动分离且分离区不断扩大的因素。在Slice-2到Slice-4剖面中心线周围存在横向速度分量(左侧向左而右侧向右),这是阀板对流动阻挡作用影响减弱、中心线上发生离心的流体质点与周围流体质点流动剪切的结果。另外,Slice-2到Slice-4剖面图可见一对涡团(左侧逆时针、右侧顺时针),这是弯管中流体质点二次流的表现。
当阀门角度为15°时,Slice-1剖面中心线上观察不到向上的速度矢量,这是因为阀板迎流面与管道间通流截面扩张较小且二者通流截面最小值(喉部)处靠近阀板后缘,从而造成阀板对流体质点的流动引导作用不明显导致的;相比之下,阀板左侧通流截面扩张较大且喉部距离后缘较远,因而阀板背流面对流体质点向管道内侧的流动引导较为明显;基于以上两点以及流体在弯管内外侧压力的共同作用下,Slice-1剖面中心线上的速度矢量均向下。另外,在Slice-1剖面中存在2对旋向相反的涡团,其中一对涡团(左侧顺时针,右侧逆时针)是阀板对流体质点的流动阻挡引起的,结论一致;而另一对涡团(左侧逆时针,右侧顺时针)则是弯管内侧与阀板迎流面间流体质点二次流所导致的。随着流体质点继续向后流动,Slice-2到Slice-4中心线速度矢量均向上,这与阀门角度为0°时的情况相同。同时从Slice-2到Slice-3可以看出,阀板流动阻挡作用形成的涡团在二次流涡团的流动剪切下逐渐削弱,且后者影响范围逐渐扩大,并在Slice-3上达到最大值;这说明此时阀板对流体质点的流动阻挡作用越来越弱,而流体质点二次流越来越强。Slice-4中心线向上的速度矢量则包含弯管内侧附近流体质点流动分离的因素。
当阀门角度为30°时,从中截面速度矢量图可知,阀板背流面与管道外侧间的流体质点因阀板引导作用而使得速度矢量向右向上,而迎流面与管道内侧间的流体质点也因同样原因使得速度矢量向右向上,因而Slice-1的中心线速度矢量均向下。同时Slice-1中,因阀板对流动的阻挡作用,两旁形成了一对涡团(左侧顺时针,右侧逆时针),在后续各剖面图中均存在。在Slice-2中,阀板背流面与管道外侧间流团的离心作用及阀板两侧流团的相互碰撞导致中心线上部流体速度矢量向上,下部流体速度矢量向下;而具有向上速度矢量的流体质点与阀板阻挡流动形成的那对涡团中心侧流体质点的流向相反,由于流动剪切作用,在后者靠近中心线侧又形成了一对涡团;且由于离心作用及流动剪切碰撞,该涡团不断上移,这从Slice-2到Slice-4剖面中也可以看出。在Slice-3剖面中心线下部具有向上的速度分量,这是由于弯管内侧流体质点的流动分离作用,因而这股流团与因流动碰撞形成具有向下速度分量的流体质点发生再次碰撞而形成一对涡团(左侧顺时针,右侧逆时针),这些发生分离的流体质点在Slice-4下方亦表现为向上的速度矢量。
当阀门角度为45°时,由于与阀门角度为30°时相同的原因,Slice-1的中心线速度矢量均向下。但由于此时来流攻角较大,更易产生逆压梯度,因而从中截面矢量图可以看出,阀板背流面前段存在一个明显的分离区;同时可以看到,阀板尾流区存在一条较为明显的流动分界线,以及管道内侧高速流体对外侧与其接近的左侧低速流体的卷吸混合现象,这是因为两侧速度大小差别较大,右侧流团表现出射流现象,该作用一直延续到Slice-4。同时各剖面中还存在一对阀板阻挡流动的流动涡团(左侧顺时针,右侧逆时针)。在Slice-2到Slice-4中,除阻挡流动的涡团外,还存在一对二次流涡团(左侧逆时针,右侧顺时针),并在Slice-3中影响范围达到最大。同时,由于弯管内侧对通过阀板迎流面与管道内侧间流体良好的流动引导作用,因而其他阀门角度下由于流动分离引起的Slice-3和Slice-4中弯管内侧向上的速度矢量,在该角度下消失。由此可见,4种阀门角度下中截面及各剖面速度矢量图差别较大,因而阀门角度对流场影响较大,其中蕴含着流动分离、弯管二次流以及流动剪切碰撞等复杂流动现象。
3.2.2 驻点和流动分离分析
从图5可以看出,当阀门角度为0°时前驻点几乎在阀板前缘点,随着阀门角度变大,阀板前驻点p逐渐向阀板中心移动,x轴坐标分别为0、-0.14d、-0.17d和-0.21d。
对阀板背流面而言,一次分离区(L1)随阀门角度的增大而增大,这是因为随来流攻角的增大,前缘逆压梯度增大,因而更易发生分离。另外,由于阀板背流面与管道外侧间通流截面扩张加重,更易产生逆压梯度,因而二次分离区更易出现。在前3种角度下,一、二次分离区不是很明显;当阀门角度从30°变为45°时,一、二次分离区将显著变大。
当阀门角度为0°时,阀板右侧通流截面的扩张以及弯管内外压差导致逆压梯度的出现,因而在扩张段靠近尾部区域出现了较为明显的流动分离区(L3)。阀门角度为15°时的情况与0°时相似,但分离区(L3)减小,这主要是阀板右侧通流截面扩张减缓的表现;当阀门角度为30°和45°时,由于阀板右侧通流截面不存在扩张段,以及管道内外压差作用减弱,没有出现流动分离现象。
另外,由于阀板后缘的几何形状(扇形圆弧),两侧流体质点会因通流截面的突然扩大而发生分离,表现为出现一对反向涡团(L4和L5)。但阀门角度为0°时,右侧阀板通流截面扩张段的流动分离涡团(L5)与后缘产生的分离涡团相混合,共同表现为L3。而阀门角度为45°时背流面第二分离区的存在抑制了左侧涡团的产生,并影响到右侧涡团的大小,因而L4和L5均很小。可见,由于阀板复杂的几何型线、弯管的存在以及阀门角度的不同,阀板后缘流动分离状况较为复杂。
由此可知,随阀门角度的增大,迎流面前驻点逐渐向中心移动,一、二次分离区更易产生,且当阀门角度从30°变为45°时,一、二次分离区将显著变大。
3.2.3 中截面云图
图7给出了不同阀门角度下中截面速度和压力云图。从图7可知,模型最大速度随阀门角度的增大而增大。当阀门角度为0°时,由于阀板两侧与管道内外侧间喉部面积较大以及阀门流线型阀板,因而前缘周围区域速度整体低于弯管内侧附近区域,且由于流体质点向心运动,弯管内侧附近区域存在整个模型的最大速度。当阀门角度为15°时,阀板前缘由于流动分离造成分离区外速度较高,且其作用强于管道内侧流体质点向心运动引起的速度增加,因而最大速度转移至阀板前缘附近区域。同理,当阀门角度为30°时,最大速度也分布在该区域,但此角度下由于通流截面变化与阀门角度为15°时不同,因而速度出现阀板右侧递增而左侧分离区外递减的趋势。当阀门角度为45°时,由于阀板与管道内侧间喉部通流截面较小,且喉部流出的高速流体在管道内侧进一步加速,因而最大速度转移回弯管内侧附近;此时阀板背流面形成较大范围低速区域,这是此处流动分离低速区的表现。
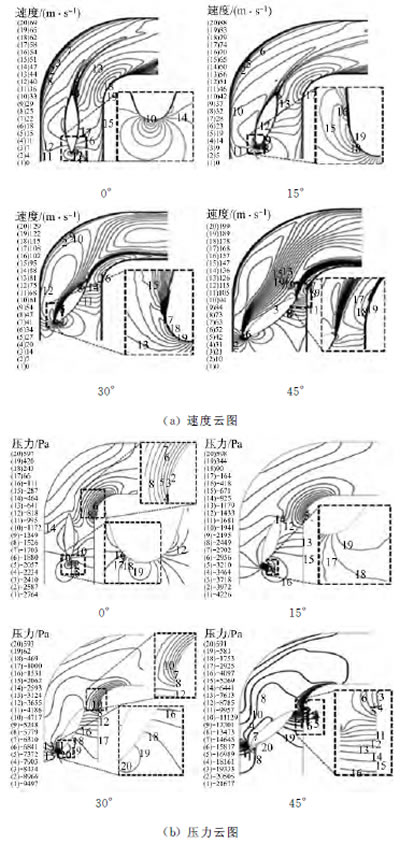
图7 不同阀门角度下中截面速度和压力云图
从图7还可以看出,模型最低压力随阀门角度的增大而降低,阀板与管道间通流面积与压力是正相关的。当阀门角度为0°时,阀板左侧通流区域压力高于右侧通流区域,这是左侧区域与弯管外侧高压区接近,而右侧区域与弯管内侧低压区接近的结果;弯管从外向内的压力梯度提供了流体质点向心作用所需的压差,最低压力出现在管道内侧。当阀门角度为15°时,模型最低压力在阀板前缘入口附近,即速度最大处。当阀门角度为30°时,由于阀板与管道间通流截面的变化,压力与速度出现相反的变化趋势,且最低压力也出现在阀板前缘附近。当阀门角度为45°时,由于最大速度转移至弯管内侧附近区域,因而最低压力出现在该处;同时背流面由于存在较大范围的流动分离,因而形成大范围低压区,且模型最低压力为阀门角度30°工况下的2.3倍。
图8给出了不同阀门角度下中截面湍动能云图。从图8可以看出,随着阀门角度的增大,湍动能不断增大。当阀门角度为0°时,阀板尾流区和弯管内侧分离区湍动能值较大,且最大值出现在弯管内侧分离区。这是因为此时阀板前缘导流作用较好而后缘较差,造成后缘流动分离较大,因而湍动能较大,但此湍动能仍小于弯管内侧的分离造成的湍动能。当阀门角度为15°时,由于具有一定攻角的来流造成前缘流动分离,而后缘由于偏向管道内侧对流动有一定引导作用,因而尾流区湍动能减小;同时,后缘的引导作用又减小了管道内侧的流动分离区,因而最大湍动能出现在阀板前缘周围。当阀门角度为30°时,阀板前缘与尾流区存在较大湍动能,且最大湍动能位于背流面前缘,这是来流大攻角导致较大流动分离的表现。当阀门角度为45°时,阀板背流面后存在更大范围的高湍动能区,且最大湍动能值存在于靠近管道内侧的尾流区,其值为阀门角度30°时的4.3倍,这可以通过阀板后缘尾流分离、阀板迎流面与管道喉部出口高低速流团形成射流的卷吸混合作用以及弯管对流体向内侧的引导作用等解释。

图8 不同阀门角度下中截面湍动能云图
可见随阀门角度的增大,模型最大速度和湍动能将增加,而最低压力降低,且各参数分布将发生显著变化,阀门角度对流场影响较大。当阀门角度从30°变为45°时,模型最低压力和最大湍动能急剧变化,45°时的最低压力和最大湍动能分别为30°时的2.3倍和4.3倍。
3.2.4 扭矩和进出口压差
表2给出了各阀门角度下阀板扭矩和进出口压差。从表2可知,随着阀门角度的增大,阀板扭矩和进出口压差将增大。当阀门角度为0°时,由于迎、背流面压力较为对称,因而扭矩较小,阀板前缘攻角最小,对流动阻挡作用不大,因而进出口压差也较小。当阀门角度为15°时,阀板两侧通流截面收缩和扩张的不同导致了两侧压力分布的不同,因而扭矩增大;同时阀门后缘表现出对流动向弯管内侧一定程度的引导,但前缘流动攻角的增大导致较大的流动阻力,因而进出口压差增大。同理,当阀门角度为30°时进出口压差和扭矩逐渐增大。当阀门角度为45°时,阀板背流面发生了严重的流动分离,形成了大范围低压区,引起阀板两侧压力分布严重不均,因而阀板扭矩也急剧增大。同时流动分离产生了涡团并造成能量损失,因而进出口压差急剧增大。阀门角度为45°时的阀板扭矩和进出口压差分别为阀门角度30°工况时的2.5倍和3.6倍。
表2 各阀门角度下阀板扭矩和进出口压差
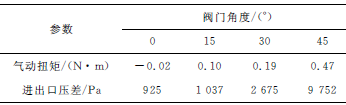
由此可知,随着阀门角度的增大,模型进出口压损增大,故而其对流动阻挡作用增大。
4 结论
(1)SST湍流模型能够获得与实验测量值最相符的扭矩计算结果。
(2)进口雷诺数对流场的影响是定量而非定性的。随进口雷诺数的增大,扭矩值具有增大趋势,阀板迎流面前驻点位置保持不变(x轴坐标为-0.21d),背流面一、二次流动分离区不断减小,一次分离区再附点x轴坐标从-0.11d逐渐变为-0.16d。
(3)阀门角度对流场的影响是定性的,可通过流动分离、弯管二次流以及流动剪切碰撞等理论进行解释。在所选的4种阀门角度中,阀门角度越大,阀门对流动的阻挡作用越大,阀板前驻点逐渐向阀板中心移动,x轴坐标分别为0、-0.14d、-0.17d和-0.21d。背流面更易产生一、二次分离区。
(4)当阀门角度从30°变为45°时,相关参数将发生急剧变化,阀板扭矩、进出口压差、最大湍动能和最低压力分别增加1.5倍、2.6倍、3.3倍和1.3倍,同时将发生较为显著的一、二次流动分离现象。

会员咨询:
客户服务:
友情链接:









