流量测量是计量科学技术的重要组成部分,它已经被广泛应用于工农业生产、环境保护、科学研究、对外贸易、人民生活等各个领域,准确快速的流量测量对于保证产品质量、提高经济效益、节约能源、促进科学技术的发展等具有重要的作用。在能源危机日益凸显的时代,流量测量在国民经济中的地位与作用越来越重要。
流量测量作为工业过程中关键的技术之一,一直受到广泛的关注和深入的研究.常见的流量测量计包括差压流量计、容积式流量计、转子流量计、电磁流量计、超声波流量计、科里奥利流量计等,其中又以差压式流量计研究最广泛。
差压式流量计是根据安装于管道中流量检测件产生的差压、已知的流体条件和检测件与管道的几何尺寸来测量流量的仪表。差压式流量计由一次装置和二次装置组成。
调节阀是管道系统中一种阻力可变的元件。通过改变阀门的开度,可以改变管道系统的工作特性,从而实现调节流量和改变压力的目的。调节阀在石油、化工、电站、长输管线等国民经济部门中是不可缺少的流体控制设备。相对于其他基础工业装备如泵、压缩机等,调节阀结构较简单,因此常不被重视。
差压式流量计有着悠久的研究历史,若将其流量测量原理运用到调节阀上,会是一项有意义的工作。利用管道中原有的调节阀设备,不增加额外阻力件的差压式流量测量方法,可以避免不必要的管道压力损失,具有一定的研究价值。
1 测量原理
对于某开度下的调节阀,其压力降的计算公式可以写成:
 (1)
(1)
式中:ρ—介质密度;υ—指在调节阀之前或之后,按管径计算的流体平均速度;ζ—通过阀门的能量损失系数。
在式(1)基础上,可以得出通过调节阀的流体流量计算公式如下:
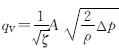 (2)
(2)
式中:A—管道的截面积。
在式(2)中,令
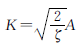 (3)
(3)
则式(2)可以写成:
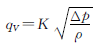 (4)
(4)
式中:K—只与调节阀的结构和开度有关的参数。
从式(4)可获得K的表达式:
 (5)
(5)
引入K的目的是确定调节阀特性.如果令Δp=100kPa,ρ=1000kg/m3,那么,在数值上K=qV。在这种标准情况下,K用符号KV表示,即调节阀的流量系数。可见,KV值与调节阀所在的管路系统无关,只与调节阀的结构和开度有关。对于某特定调节阀,其结构是一定的,那么则有关于KV的函数:
KV≡KV(H) (6)
式中:H—调节阀的开度。
式(6)表达了调节阀的流量特性。
流量特性KV很容易通过实验精确确定,通过在标准条件下测量通过调节阀的流量即可确定。
调节阀的开度为100%时的KV值写作KVmax,KV/KVmax叫做相对流量。通过实验测量调节阀不同开度下的相对流量,绘制成相对开度-相对流量曲线,即调节阀的流量特性曲线。显然,知道调节阀的相对开度,就可以通过流量特性曲线获得此开度下的KV值。
以下给出利用调节阀的流量特性曲线和调节阀前后差压,计算通过调节阀的流体流量的计算公式。在标准条件下,式(2)写成:
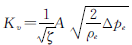 (7)
(7)
将式(2)和式(7)两式相比,得到:
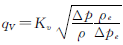 (8)
(8)
标准条件参数值分别为Δpe=100kPa,ρe=1000kg/m3,代入式(8)中,得:
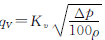 (9)
(9)
由式(9)可见,流过调节阀的流体流量,只与调节阀当前开度下的KV值、调节阀前后的差压、流经的流体的密度有关。KV值可以由调节阀的当前开度和流量特性曲线获得,流体密度一般已知,流量测量工作实际转变为调节阀前后的压力测量工作.
2 实验系统
实验系统整体设计如图1,关键设备包括电动单座调节阀、多个压力变送器、Agilent34970a数据采集开关、计算机、作为标准流量计的电磁流量计、水泵、调节水泵的变频器、容积式流量计、储水池等。
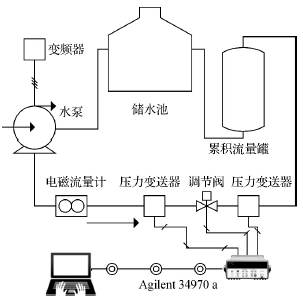
图1 实验系统示意图
变频器调节水泵的出力,水泵将储水池内的水打入管道系统。首先,水流流经电磁流量计,就地读出瞬时流量值。然后,水流流经阀前压力变送器、调节阀、阀后压力变送器,由Agilent34970a采集到阀前压力信号、调节阀开度信号、阀后压力信号,并通过串口通信提交给计算机;同时,计算机通过串口通信发送阀位调节命令给调节阀执行机构,执行机构改变调节阀开度。当水流到达累积流量罐上游时,可以流入累积流量罐进行累积流量测量;也可以从旁路绕过累积流量罐,直接进入储水池。最后水流回到储水池,进行循环利用。表1列出了部分设备的性能参数。
表1 部分设备性能参数

Agilent官方提供了BenchLink软件,可方便地在计算机上进行数据的采集和保存,但是并不能满足本实验系统的需求。通过自己设计配套软件,在采集方面可以做到多点同时采集、设定自动采集频率、后台直接完成原始信号到最终量的换算,数据保存到文件等;而在控制方面,不但可以发送单个的阀位控制信号,还可以编程实现阀位控制信号序列的连续发送,并利用多线程技术在一台Agilent 34970a上同时进行采集与控制操作。
3 实验结果与分析
3.1 压力采样点的选定
调节水泵变频器,待到电磁流量计读数稳定到38.49m3•h-1左右时,以1s的时间间隔开始同时采集六个压力变送器(阀前阀后各三个,距离调节阀法兰距离为1D、3D、5D,从前到后依次编号为1~6)的电压信号,采集约1min后停止,获得每个压力变送器的平均电压、最大电压、最小电压、均方差,绘制为图2。
如图2,对于阀前压力,3号采样点数据的误差范围最小,均方差也最小;对于阀后压力,5号采样点数据的误差范围最小,均方差也最小。流体通过调节阀内的复杂结构时,容易产生紊流,需要经过一段直管段后才能渐渐稳定,故下游压力采样点相对较远。最终,分别选定3号压力采样点和5号压力采样点为阀前、阀后压力采样点,也确定了上游压力采样点相对靠近调节阀,下游压力采样点相对远离调节阀的压力采样点选定原则。
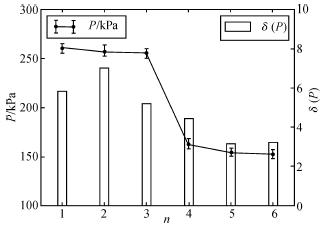
图2 压力采样点的选定实验结果
3.2 调节阀的流量特性曲线
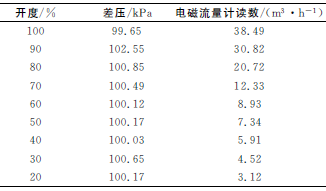
表2列出了标准情况下,调节阀不同开度下的流量值,即流量系数KV值。
表2 流量特性曲线实验数据
根据以上实验数据,绘制了如图3的调节阀的流量特性曲线。曲线形状与调节阀标称的等百分比流量特性一致。
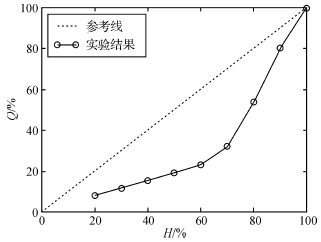
图3 流量特性曲线
3.3 稳态流量测量实验
选取较有代表性的78%和35%一大一小两种开度进行了稳态流量测量实验,实验数据见表3。可以看到,最大相对误差为4.46%,最低为0.2%,测量精度较好。
表3 稳态流量测量实验数据
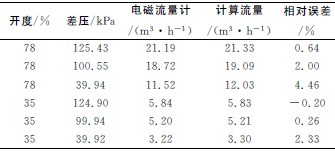
图4为当开度一定时,差压与相对误差的关系。针对78%较大的阀门开度,还是35%的较小开度,当差压较小时,相对误差总是偏大;而差压较大时,相对误差则变小。该结果表明,当应用基于调节阀的流量测量方法时,阀前后的差压大小会影响测量的精度。由于开度一定时,通过调节阀的流体流量是随差压的增大而增大,因此开度不变时,在进行小流量测试时,误差会增加。
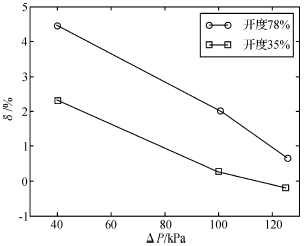
图4 差压与相对误差的关系
图5为当差压一定时,开度与相对误差的关系。可以看到,在40kPa、100kPa、125kPa三种差压条件下,开度较小时,相对误差较小;开度较大时,相对误差较大。该结果表明,应用基于调节阀的流量测量方法时,调节阀开度不同也会影响测量精度。由于阀前后差压一定时,通过调节阀的流体流量随着阀门开度的增大而增大,表明差压不变,大流量即增加阀门开度时误差会增加。
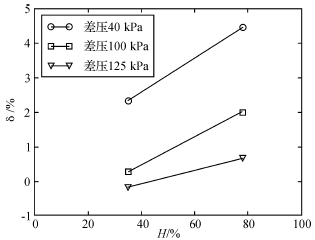
图5 开度与相对误差的关系
综合开度一定、差压一定时的相对误差变化特点,可以发现较大的阀前后差压,较小的阀门开度,是基于调节阀的流量测量方法的测量精度最佳的工况。同样,分析结果也表明,稳态工况下的流量测量相对误差与流量的大小无直接对应关系。
3.4 非稳态流量测量实验
图6为正弦信号作为阀门开度输入信号时,相对开度与阀前后差压呈相反的变化趋势。当水泵的出力不变时,调节阀相对开度一旦变小,流经调节阀的流量会变小。如果没有调节阀KV值的变化,阀前后的差压也应该随着流量的变小而变小;但是,由于相对开度的变小,KV值也变小了,且对阀前后差压变化的影响较大,所以出现了流量变小,差压反而增大的结果。
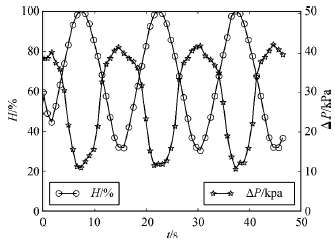
图6 正弦信号时相对开度和阀前后差压
在时间为15s时,阀前后差压达到了极大值。可以看到,在此极值前,阀前后差压的变化速率明显变缓。这是由于时间接近15s时,调节阀的相对开度从最大时的100%逐渐减小到了30%。实验所用的调节阀为等百分比流量特性,如图3所示。在小开度时的流量特性曲线斜率要明显比大开度时小。所以,图6中的两条曲线形状并没有完全对称。
通过图7可以看到,正弦信号作为阀门开度输入信号时的流量变化基本与调节阀相对开度的变化所一致。时间为15s时,调节阀相对开度达到极小值(调节阀设置为失电全开),流经调节阀的水流量也达到极小值。曲线的极大值处发生了明显的畸变,出现了一个倒齿。这表明,调节阀开度在由小变大,转为由大变小时,基于调节阀的流量测量方法所测得流量值出现波动。波动原因可能是阀芯运行反向带来更大的阀内流体扰动,进而影响到阀前后压力采集精度。

图7 正弦信号时流量
对图7中的流量随时间变化曲线进行数值积分,可以计算得到这段时间流经调节阀的流体累积流量为197.24×10-3m3。另外,容积式流量计所测得的对应累积流量为195.04×10-3m3,将其作为参考值。基于调节阀的流量测量方法,在阀芯按正弦信号开关的工况下,累积流量误差仅为1.13%。
从图8和图9可以看到,虽然随机信号时相对开度的变化无规律,但流量的变化基本与相对开度的变化趋势保持一致。

图8 随机信号时相对开度和阀前后差压

图9 随机信号时流量
在时间40s附近,开度的变化规律类似于正弦信号,流量变化曲线也出现了预料中的倒齿。
对图9中的流量随时间变化曲线进行数值积分,可以计算得到这段时间流经调节阀的流体累积流量为206.38×10-3m3。另外,容积式流量计所测得的对应累积流量为200.72×10-3m3,将其作为参考值。基于调节阀的流量测量方法,在阀芯按随机信号开关的工况下,累积流量误差为2.82%。
4 结语
首先提出将差压式流量计测量原理应用于调节阀的流量测量方法,建立了相应的实验测量装置.随后通过稳态和非稳态流量测量实验,得到了定量化分析结论,并分析了测量误差来源。最后证明该方法简便易行,在工程上具有良好的应用价值。



会员咨询:
客户服务:
友情链接:
 (1)
(1)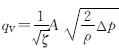 (2)
(2)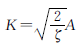 (3)
(3)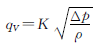 (4)
(4) (5)
(5)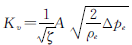 (7)
(7)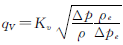 (8)
(8)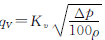 (9)
(9)










